Remainder Theorem
and Factor Theorem
Or: how to avoid Polynomial Long Division when finding factors
Do you remember doing division in Arithmetic?
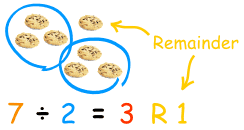
"7 divided by 2 equals 3 with a remainder of 1"
Each part of the division has names:
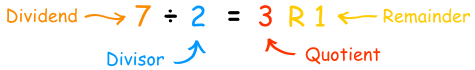
Which can be rewritten as a sum like this:
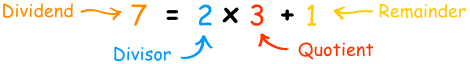
Polynomials
Well, we can also divide polynomials.
f(x) ÷ g(x) = q(x) with a remainder of r(x)
But it is better to write it as a sum like this:
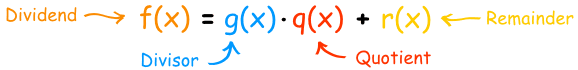
Like in this example using Polynomial Long Division:
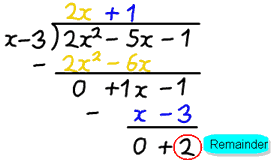
No comments:
Post a Comment