Fractions

A fraction is a part of a whole

Slice a pizza, and we get fractions:

1/2	1/4	3/8
(One-Half)	(One-Quarter)	(Three-Eighths)

The top number says how many slices we have. 
The bottom number says how many equal slices it was cut into.

Have a try yourself:

Click the pizza →

Slices we have:

Total slices:

"One Eighth"

Slices:

Equivalent Fractions

Some fractions may look different, but are really the same, for example:

4/8	=	2/4	=	1/2
(Four-Eighths)		Two-Quarters)		(One-Half)
	=		=

It is usually best to show an answer using the simplest fraction ( 1/2 in this case ). That is called Simplifying, or Reducing the Fraction

Numerator / Denominator

We call the top number the Numerator, it is the number of parts we have.
We call the bottom number the Denominator, it is the number of parts the whole is divided into.

Numerator

Denominator

You just have to remember those names! (If you forget just think "Down"-ominator)

Adding Fractions

It is easy to add fractions with the same denominator (same bottom number):

1/4	+	1/4	=	2/4	=	1/2
(One-Quarter)		(One-Quarter)		(Two-Quarters)		(One-Half)
	+		=		=

Another example:

5/8	+	1/8	=	6/8	=	3/4
	+		=		=

Adding Fractions with Different Denominators

But what about when the denominators (the bottom numbers) are not the same? 

3/8	+	1/4	=	?
	+		=

We must somehow make the denominators the same.

In this case it is easy, because we know that 1/4 is the same as 2/8 :

3/8	+	2/8	=	5/8
	+		=

But when it is hard to make the denominators the same, use one of these methods (they both work, use the one you prefer):

• Least Common Denominator, or
• Common Denominator

taken from  https://www.mathsisfun.com/fractions.html

Quick Tricks for Multiplication

Quick Tricks for Multiplication



Why multiply?

A computer can multiply thousands of numbers in less than a second.  A human is lucky to multiply two numbers in less than a minute.  So we tend to have computers do our math. 

But you should still know how to do math on paper, or even in your head.  For one thing, you have to know a little math even to use a calculator.  Besides, daily life tosses plenty of math problems your way.  Do you really want to haul out Trusty Buttons every time you go shopping?

Of course, normal multiplication can get boring.  Here's the secret: shortcuts.  You might think of numbers as a dreary line from 0 to forever.  Numbers do go on forever, but you can also think of them as cycles.  Ten ones make 10.  Ten tens make 100.  Ten hundreds make 1000.  

If numbers were just a straight highway, there'd be no shortcuts.  But they're more like a winding road.  If you know your way around, you can cut across the grass and save lots of time.

Multiply by 10: Just add 0

The easiest number to multiply by is 10.  Just “add 0.”

3 x 10 = 30 140 x 10 = 1400 

Isn't that easy?  This “trick” is really just using our number system.  3 means “3 ones.”  Move 3 once to the left and you get 30, which means, “3 tens.”  See how our numbers cycle in tens?  Whenever you move the digits once to the left, that's the same as multiplying by 10.

And that's the quick way to multiply by 10.  Move each digit once to the left.  Fill the last place with a 0.  


Math: Quick Tricks for Multiplication

Name: _____________________________________________________


2 ©2005abcteach.com
Exercise A:   1. Give two reasons to get good at doing math in your head.


2. Give two situations where you might need or want to do math in your head, not with a calculator.


3. Explain the quick way to multiply by ten.  


4. Solve these problems without using a calculator. a. 4 x 10 

b. 15 x 10

c. 400 x 10

d. 23 x 10

e. 117 x 10

Taken from  http://www.abcteach.com/free/m/mulitplication_quicktricks_elem.pdf

Sums of powers

Sums of Powers - A Festive Story

Article by Theo Drane

Published November 2006,December 2006,February 2011.

On the twelfth day of Christmas, my true love gave to me.. .

How many gifts?
But that's easy; all you have to do is add up the numbers from one to twelve.

That sounds easy, but what if the last line had been... fifty drummers drumming?
Isn't there a better way than huddling over your calculator?

And a partridge in a pear tree...

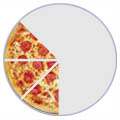
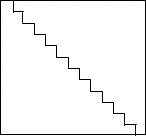
On the fifth day 1+2+3+4+5=15 gifts are given. We can visualize this as 15 squares arranged into the shape of a staircase; 1 square on top of 2 squares on top of 3 squares etc.

Two of these staircases can be placed together to form a rectangle. The stair shape is half the area of the rectangle, which is:

5×(5+1)2=15

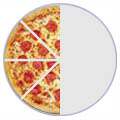
For the twelfth day we can repeat the process and end up with a new rectangle, as shown on the right. The rectangle is 12 by 12+1=13. We can now say: 

1+2+3+...+12=12×(12+1)2=78

So the true love gets 78 gifts on the twelfth day of Christmas.

How many gifts arrive on the nth day?

The same argument applies and we would end up drawing a rectangle that was nsquares high and n+1 squares wide. We would end up with: 

1+2+3+...+n=n×(n+1)2

Four turtle doves...

That's all well and good but what if the true love went overboard on the whole gift front?

Instead of two turtle doves, he gave four;

instead of three French hens he gave nine ...

More precisely, if instead of giving n gifts on the nth day, n×n (normally written as n2) gifts are given, then what?

Now on the twelfth day there would be 1+4+9+25+…+144 gifts.

Is it time to huddle over our calculator now?

Not quite yet, we can visualize the number of gifts on the third day, for example as 1 cube on top of 4 cubes on top of 9 cubes arranged as in Figure A.

Now treat the object in A as a single building block. If you put two of these building blocks together you get the solid in Figure B.

Adding another building block you get the solid on the left in Figure C. The picture on the right is just a different view of the solid shown on the left.

Figures D and E show two copies of the solid made from three building blocks separately (D) and then placed together (E).

Now what is the point of all this?

Well the task is to work out how many cubes are inside our building block, we can do it two ways.

By direct counting we get:

1+4+9=14.

But we also have shown that six of our building blocks can be arranged into the solid cuboid in Figure E. So, how many cubes are there in Figure E?

Well the cuboid is 3 cubes high, 4 cubes wide and 7 cubes long and the cuboid contains 6 of our building blocks.

So the volume of our building block is: 

1+4+9=3×4×76=14

Now here's a question:

Would the construction have worked if our building block had more layers, e.g. 1 cube on top of 4 cubes on top of 9 cubes on top of 16 cubes?

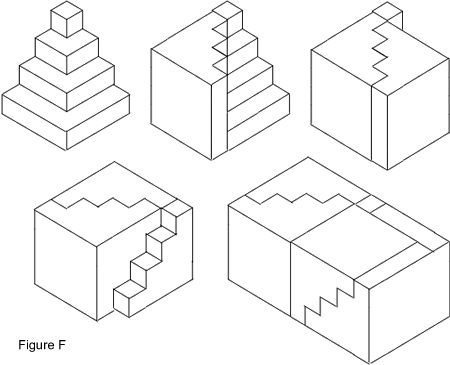
We can repeat the process, but this time starting with a block with four layers.

The final solid in Figure F is now a cuboid that is 4 cubes high, 5 cubes wide and 9 cubes long and the cuboid contains 6 of our building blocks.

So in this case the volume of the building block is 

12+22+32+42=4×5×96=30

By staring at the images, I hope you would agree that we can start with a building block that has any number of layers and that following the same construction we would end up with a cuboid that is n blocks high, n+1 cubes wide and 2n+1 cubes long and contains 6 our of building blocks.

So then the volume of the building block would be 

12+22+32+…+n2=n×(n+1)×(2n+1)6

So our overzealous gift giver would have bestowed 

12×13×256=650

gifts on his true love on the twelfth day.

N.B. You can find an algebraic proof of this result in the article "Mathematical Induction" on the site.

Twenty-seven French hens ...

You may now have an inkling as to where this is heading:

what if instead of two turtle doves, he gave eight

and three French hens became twenty-seven?

Demonstrations of the following result in this article can be found but are not included here, for example you can look at the problem "Picture Story" .

13+23+…+n3=(1+2+3+…n)2

A very pleasing result which means that ...

On the twelfth day our exhausted distributor of gifts would have dispensed:

13+23+…+123=(1+2+3+…12)2=6048gifts.

Two hundred and fifty-six calling birds and more ...

So why stop there?

Well, if you are feeling a bit taxed and want to stop here, I think I have given you enough to think about.

For the rest of you intrepid explorers who want to carry on to the summit, for a whole number n and m, go to the notes for more and more and more...

                                                              Article taken from

                                                                   http://nrich.maths.org/5435